Wat een naar spel. Daarom ga ik het kapot analyseren zodat ik niet meer uitgelachen kan worden om mijn matige reactiesnelheden. (En het feit dat ik als wiskundige belachelijk slecht kan tellen.)
Oftewel, we gaan kijken of je kan winnen zonder dat reactiesnelheid een rol speelt. Bijvoorbeeld, door gewoon standaard om de drie kaarten op de bel te slaan.
De Spelregels
Er is een stapel met kaarten. Op een kaart is een fruitsoort afgebeeld (er zijn er 4 in totaal), in een bepaalde hoeveelheid (1 t/m 5). Deze stapel wordt opgedeeld onder de spelers. Zij leggen die gedekt voor zich. (Ook staat er een bel in het midden van de tafel.)
Om de beurt draait men de bovenste kaart van zijn stapel om, en legt die voor zich, bovenop zijn vorige open kaart.
- Als in totaal exact 5 symbolen van een bepaalde fruitsoort te zien zijn op tafel, is er een Halli Galli. Iedere speler probeert op de bel te slaan. Diegene die dat als eerste lukt, krijgt alle open kaarten, en voegt die aan zijn gedekte trekstapel toe. Hij begint de volgende ronde.
- Als er geen Halli Galli is, speelt men gewoon door. Als iemand toch foutief op de bel slaat, moet deze voor straf één kaart aan elke andere speler geven.
Als iemand geen kaarten meer heeft, is deze uit het spel, tenzij die persoon het huidige potje weet te winnen. De persoon die uiteindelijk alle kaarten heeft, wint het spel.
(Een variant is dat de laatste twee spelers nog één ronde spelen, en wie die ronde wint is de uiteindelijke winnaar. Anders kan het einde van het spel superlang duren. Looking at you, Risk.)
Opmerking: ik heb geen spel bij de hand om precies de kaarten te tellen. Ik weet dat er 56 kaarten zijn. Verdeeld over 4 vruchten, geeft dat 14 kaarten per soort. Ik ga er vanuit dat de makers zoveel mogelijk uitkomsten willen die in de buurt van 5 zitten. Dus, 3 zit er het meest in, daarna 2 en 4, en daarna 1 en 5. Ik kom zo uit op de volgende verdeling: 2, 3, 4, 3, 2.
En hoe ga jij zo’n spel analyseren?
Aha! Nu wordt het interessant. Als ik een fatsoenlijk kaartspel zou analyseren, waarbij men bijvoorbeeld uit eigen hand kiest wat men speelt, dan kan ik gewoon een simulatie maken die willekeurig 1 van de X kaarten in iemands hand kiest.
Omdat dit spel te maken heeft met reactiesnelheid—zowel het zien van een Halli Galli, als wel het succesvol slaan van de bel—kan dat niet. In plaats daarvan moet iedere speler volgens een bepaalde kansverdeling reageren. Het zou onrealistisch zijn om te zeggen dat elke speler altijd precies een halve seconde doet over op de bel slaan.
De meest bekende kansverdeling is de normaalverdeling. (De naam komt ook van dat hij zo veel wordt gebruikt dat het normaal is.) Maar die kan niet. Dan bestaat er namelijk een kans dat de reactiesnelheid negatief wordt, en het lijkt me sterk dat iemand nog voordat hij een kaart heeft gezien, weet dat het een Halli Galli wordt. (Tenzij diegene vals speelt, natuurlijk.)
Dus, wat doen we? De exponentiële verdeling! Deze wordt vrijwel altijd gebruikt als het gaat om (wacht)tijden, omdat hij altijd positief is. Een ander voordeel is dat berekeningen heel makkelijk gaan.
Een simpel spelletje
We spelen met drie spelers.
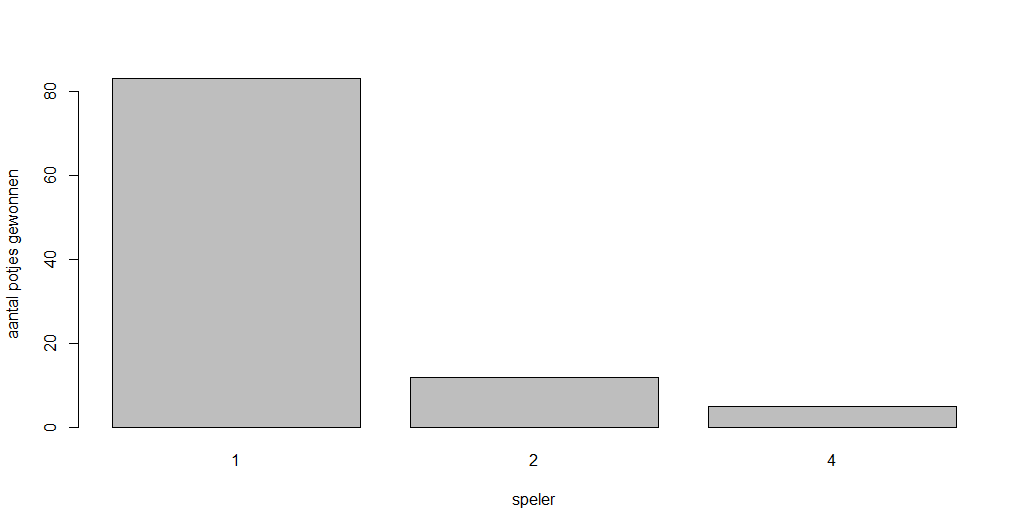
Speler 1 gaat het best, speler 2 en 4 minder goed, en speler 3 wint gewoon helemaal niks.
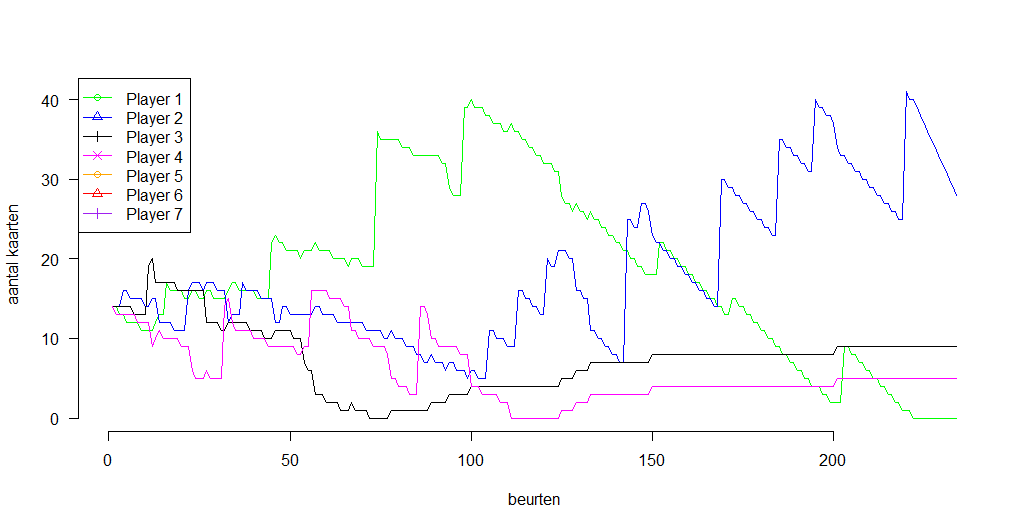
Opmerking: in de grafiek lijkt het alsof spelers terugkomen uit de dood. De regels stellen dat een speler die geen kaarten meer heeft in leven blijft totdat het huidige potje is afgelopen. Als de speler dit potje wint, namelijk, heeft ie weer kaarten en kan nog meedoen. Daarnaast zat er hier nog wel een fout in de grafiek-maak-code, maar die heb ik er pas later uitgehaald :p
Ik heb hem nog een keer gedaan, voor de zekerheid:
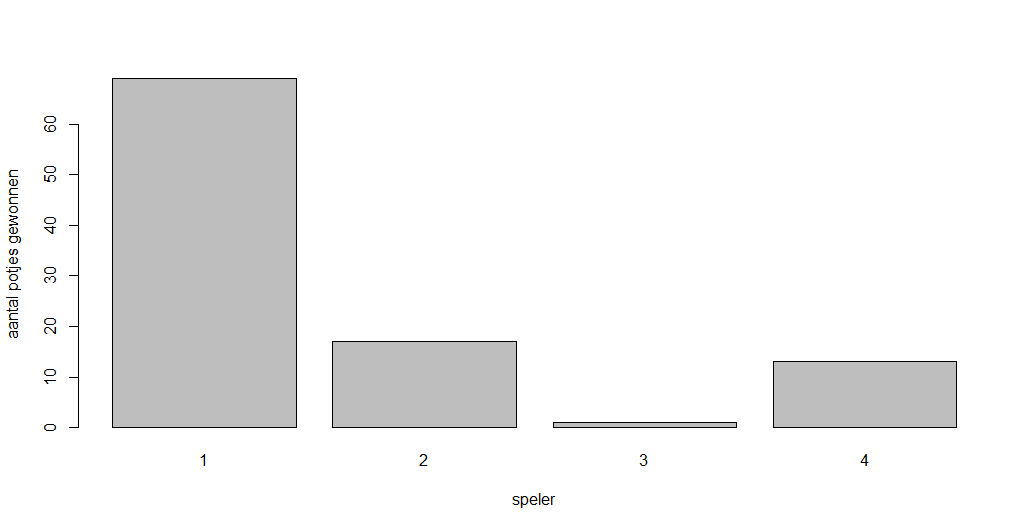
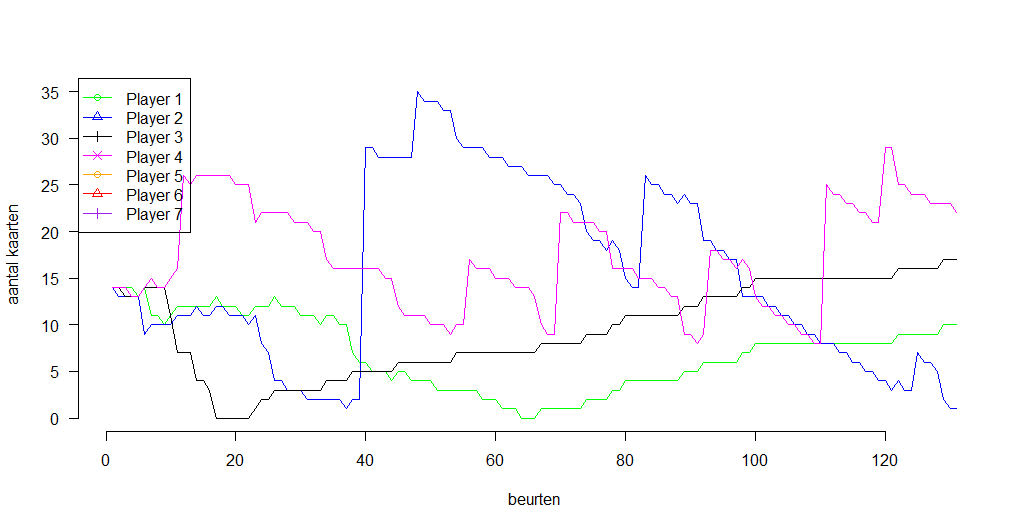
En dat geeft hetzelfde beeld. Zoals je ziet gaat onze flauwe speler 4 de hele tijd op en neer in het spelverloop (grafiek rechts)—maar in dit specifieke potje komt hij daarmee wel als winnaar uit de bus!
Hoe dan ook, speler 1 blijft de overduidelijke winnaar. Dat moet veranderen.
- We verwisselen speler 3 met een flauwe speler die elke ronde op de bel slaat wanneer de stapel 11 of meer kaarten bevat.
- We verwisselen speler 2 met een flauwe speler die om de vijf rondes op de bel slaat, alleen wanneer de stapel 11 of meer kaarten bevat.
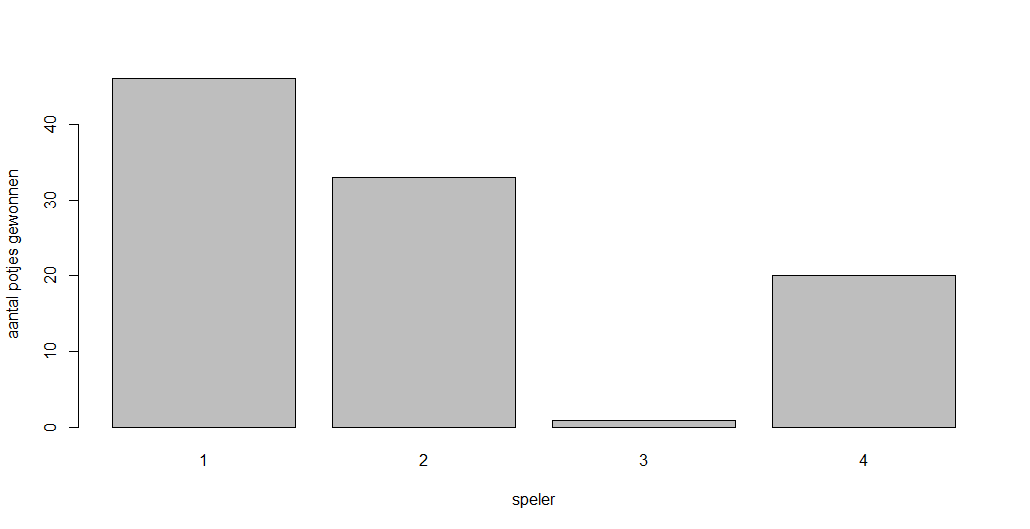
Zoals je ziet, speler 3 is niet bepaald succesvol, maar speler 2 wel degelijk! Ze slaat alleen op de bel als de stapel groot is, maar ze spreid haar kansen, en slaat alleen eens in de vijf beurten. Dat lijkt te werken. In het spelverloop zien we waarom: speler 3 gaat vrij snel ten onder, terwijl speler 2 steeds en grote slag slaat en het lang volhoudt. (De potjes worden wel lang zeg.)
Hoewel onze zeer flauwe speler die gewoon om de 11 rondes slaat (speler 4) het ook niet onaardig doet, wint speler 1 nog steeds. Dit kan beter!
De Beste Strategie
We verwisselen speler 3 met een speler die alleen speelt als de kans groot is dat er een Halli-Galli aankomt.
Hoe kan hij dat ooit weten? Kaarten tellen, en een beetje logica. Ik introduceer drie mogelijke situaties:
- Onmogelijk: Als er al (meer dan) 5 van een fruitsoort ligt, van de vorige ronde, kan er natuurlijk geen Halli-Galli komen in die soort.
- _Onwaarschijnlijk: _Als er al een 0, 1 of 4 van die soort ligt, is de kans op Halli-Galli klein.
- Waarschijnlijk: Als er 2 of 3 van die soort ligt, is de kans groot.
Dit heb ik allemaal samen gegooid in de volgende formule: sla op de bel als
Waarschijnlijk * 2 + Onwaarschijnlijk—Onmogelijk >= 4
Bijvoorbeeld, stel je speelt met z’n vieren. De vorige drie kaarten waren 2 aardbeien, 1 framboos, en 5 bananen, dan geeft de formule 1*2 + 2—1 = 3. Dus niet de bel slaan!
Anderzijds, als de vorige drie kaarten 2 aardbeien, 1 framboos en 2 bananen waren, dan geeft de formule 2*2 + 2 = 6. Dus wel de bel slaan!
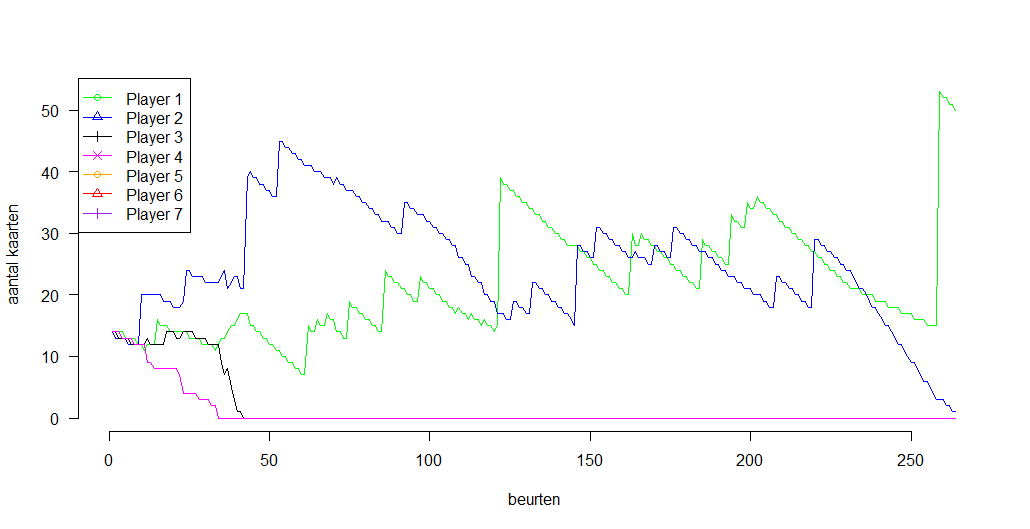
Dit is een doorslaand succes:
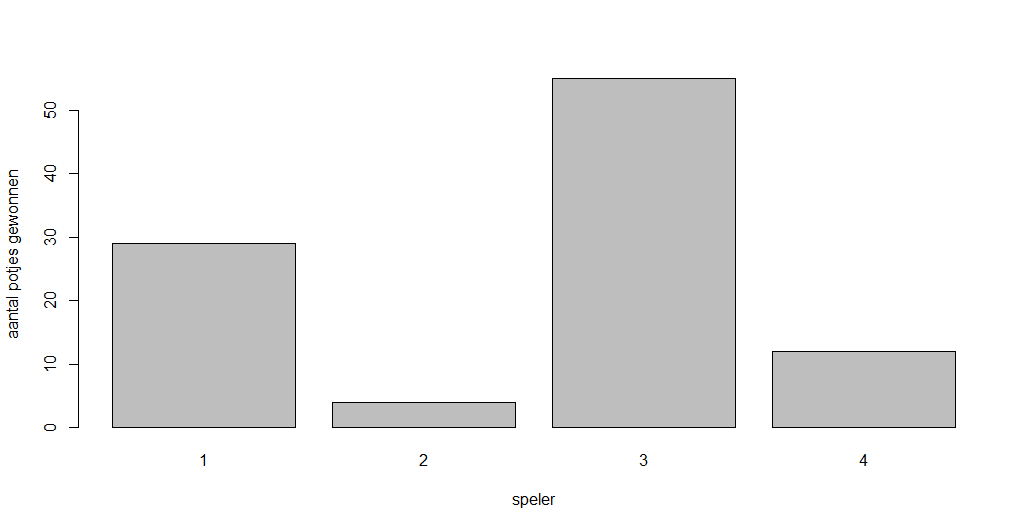
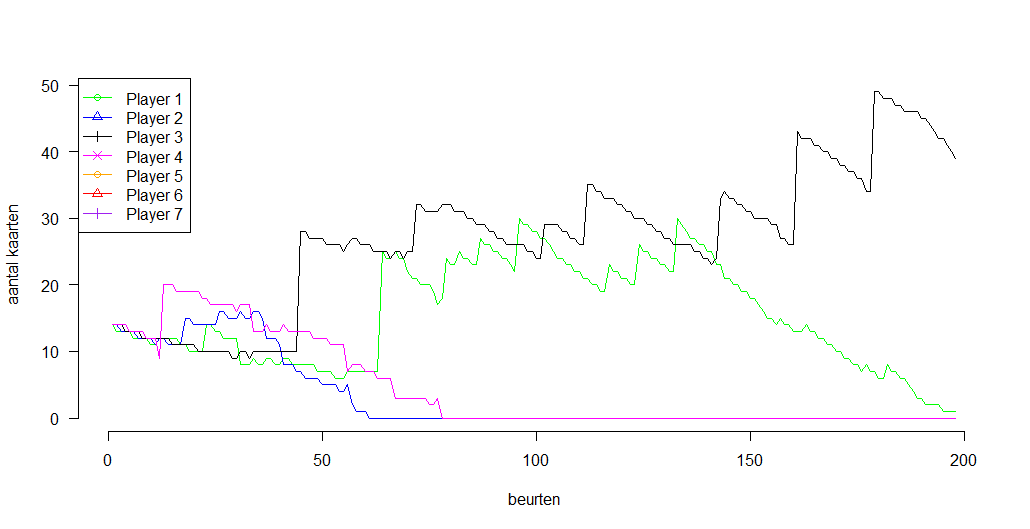
Speler 3 degradeert de rest tot amateuristische dwergen!
Wat hebben we geleerd?
Vergeet reactiesnelheid! Tel op je gemak wat er op tafel ligt, en pas de formule toe. Wanneer de volgende speler zijn kaart omdraait, sla jij gewoon alvast op de bel, zonder te zien wat het is—en meestal zul je gelijk hebben.
En dan wil niemand meer Halli Galli met je spelen. En dat is iets goeds, want dan heb je tijd over om goede en interessante spellen te gaan doen.
De Code
De code + plots zijn te vinden in deze Google Drive folder: Halli Galli (Simulatie)